Parallellepiped
En parallellepiped är en tredimensionell geometrisk figur som begränsas av sex plan, vilka två och två är sinsemellan parallella. Gränsytorna är parallellogrammer, av vilka de, som står emot varandra, är kongruenta. Parallellepipeden har tolv kantlinjer och åtta hörn.
| Parallellepiped | |
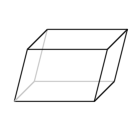 | |
| Dimensioner | 3 |
|---|---|
| Sidor | 6 |
| Kanter | 12 |
| Hörn | 8 |
Om gränsytorna är kvadrater kallas parallellepipen kub. En parallellepiped där alla sidor är rektanglar kallas rätblock. Är alla sidorna romber kallas den romboeder.
Volym
redigeraVolymen hos en parallellepiped är lika med basytans area, , multiplicerad med höjden, (se figur 1):
Basytan är en parallellogram och dess area är lika med:
- .
Höjden är lika med
Vilket ger: .
Således är volymen är lika med absolutbeloppet av den skalära trippelprodukten av de tre sidovektorerna. Detta innebär i sin tur att om kantvektorerna är:
så är volymen lika med absolutbeloppet av determinanten
det vill säga
I figur 2 visas hur man genom att skära av en röd bit i ena änden av en parallellepiped och lägga till den i den andra (då grönfärgad) kan göra sidorna rektangulära i två steg[1]. I första steget görs två par motstående sidor rektangulära, i det andra det sista paret. Eftersom den bortskurna röda biten har samma form och dimensioner som den tillagda gröna ändras inte volymen. Höjden, som markeras av den blå pilen, ändras inte heller och även den gulfärgade basytans area förblir konstant, eftersom man skär bort lika mycket som man lägger till. Således är volymen av den parallellepiped vi utgick från lika med volymen av det rätblock vi erhållit, det vill säga basytans area gånger höjden.
Area
redigeraEn parallellepiped har tre par av motstående sidor vilka är identska parallellogram. Dessa sidopar definieras av vardera två av kantvektorena. Arean av en sådan parallellogram, exempelvis den med kanterna och i figur 1, är lika med . Totalarean för en parallellepiped är således:
- .
Källor
redigera- Parallellepiped i Nordisk familjebok (andra upplagan, 1915)
- ^ Om parallepipeden har väldigt olikånga kanter och är väldigt skev kan det krävas flera parallella snitt i stegen.