Sfäriska cotangensformlerna

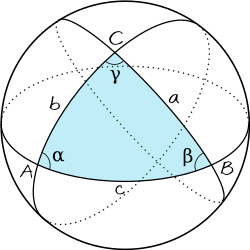
De sfäriska cotangensformlerna är en uppsättning av sex formler inom sfärisk trigonometri som säger att för fyra konsekutiva element (sidor eller hörn) i en sfärisk triangel $\triangle ABC$ med sidlängderna $a,b,$ och $c$ med de motsvarande motstående hörnvinklarna $\alpha ,\beta$ respektive $\gamma$ på en enhetssfär, som i figur 1, gäller:

Figur 1: Den sfäriska triangeln $\triangle ABC$.

$\cos b\cdot \cos \gamma =\cot a\cdot \sin b-\cot \alpha \cdot \sin \gamma$

$\cos b\cdot \cos \alpha =\cot c\cdot \sin b-\cot \gamma \cdot \sin \alpha$

$\cos c\cdot \cos \alpha =\cot b\cdot \sin c-\cot \beta \cdot \sin \alpha$

$\cos c\cdot \cos \beta =\cot a\cdot \sin c-\cot \alpha \cdot \sin \beta$

$\cos a\cdot \cos \beta =\cot c\cdot \sin a-\cot \gamma \cdot \sin \beta$

$\cos a\cdot \cos \gamma =\cot b\cdot \sin a-\cot \beta \cdot \sin \gamma$

Formlerna används för att räkna ut en andra sida när man känner två vinklar och den mellanliggande sidan eller en andra vinkel när man känner två sidor och den mellanliggande vinkeln. De är också att föredra framför den sfäriska sinussatsen i de fall de kan användas, eftersom cotangens ger entydiga resultat mellan noll och $\pi$ (och sålunda är entydig för alla Eulerska trianglar), vilket gör att man slipper det tvetydiga resultatet $\textstyle {\frac {\pi }{2}}\pm x$ som fås från arcsinus inom samma intervall, men å andra sidan är den sfäriska sinussatsen både enklare att använda och, inte minst, att minnas.

Härledning

Utgå från två av de tre varianterna av den sfäriska cosinussatsen, som:

$\cos a=\cos b\cdot \cos c+\sin b\cdot \sin c\cdot \cos \alpha$ (1) och

$\cos c=\cos a\cdot \cos b+\sin a\cdot \sin b\cdot \cos \gamma$ (2)

Ersätt $\cos c$ i (1) med (2), vilket ger (med hjälp av "trigonometriska ettan" i andra steget):

${\begin{aligned}\cos a&=\cos b\cdot (\cos a\cdot \cos b+\sin a\cdot \sin b\cdot \cos \gamma )+\sin b\cdot \sin c\cdot \cos \alpha =\\&=\cos ^{2}b\cdot \cos a+\cos b\cdot \sin a\cdot \sin b\cdot \cos \gamma +\sin b\cdot \sin c\cdot \cos \alpha =\\&=(1-\sin ^{2}b)\cdot \cos a+\cos b\cdot \sin a\cdot \sin b\cdot \cos \gamma +\sin b\cdot \sin c\cdot \cos \alpha =\\&=\cos a-\sin ^{2}b\cdot \cos a+\cos b\cdot \sin a\cdot \sin b\cdot \cos \gamma +\sin b\cdot \sin c\cdot \cos \alpha \Leftrightarrow \end{aligned}}$

$\sin ^{2}b\cdot \cos a=\cos b\cdot \sin a\cdot \sin b\cdot \cos \gamma +\sin b\cdot \sin c\cdot \cos \alpha \Leftrightarrow$ (3)

${\frac {\sin ^{2}b\cdot \cos a}{\sin b\cdot \sin a}}={\frac {\cos b\cdot \sin a\cdot \sin b\cdot \cos \gamma }{\sin b\cdot \sin a}}+{\frac {\sin b\cdot \sin c\cdot \cos \alpha }{\sin b\cdot \sin a}}\Leftrightarrow$

$\sin b\cdot \cot a=\cos b\cdot \cos \gamma +{\frac {\sin c\cdot \cos \alpha }{\sin a}}$

Från den sfäriska sinussatsen får vi $\sin a={\frac {\sin \alpha \sin c}{\sin \gamma }}$, vilket insätts:

${\begin{aligned}\sin b\cdot \cot a&=\cos b\cdot \cos \gamma +{\frac {\sin c\cdot \cos \alpha }{\frac {\sin \alpha \sin c}{\sin \gamma }}}=\\&=\cos b\cdot \cos \gamma +{\frac {\sin c\cdot \cos \alpha \cdot \sin \gamma }{\sin c\cdot \sin \alpha }}=\\&=\cos b\cdot \cos \gamma +\cot \alpha \cdot \sin \gamma \Leftrightarrow \end{aligned}}$

$\cos b\cdot \cos \gamma =\cot a\cdot \sin b-\cot \alpha \cdot \sin \gamma$

Härmed är den första av de sex formlerna härledd. Den andra formeln fås om man inledningsvis i stället ersätter $\cos a$ i (2) med (1) (och symmetrin mellan cosinussatsen för $\cos a$ och $\cos c$ gör att man strax inser att det bara innebär att $a$ byts mot $c$ och $\alpha$ byts mot $\gamma$ - det går även att visa med polära dualitetssatsen, men detta är spilld kraft), medan de fyra övriga formlerna fås om man byter ut cosinussatsen för $\cos b$ mot endera av de båda andra.

Sinus-cosinus-formlerna

Om man bara förkortar mellanledet (3) i den ovanstående härledningen av den första cotangensformeln med $\sin b$ får man

$\sin b\cdot \cos a=\cos b\cdot \sin a\cdot \cos \gamma +\sin c\cdot \cos \alpha$

Denna (och de fem andra formler som på samma sätt erhålls från motsvarande mellanled i härledningen av de fem övriga cotangensformlerna) har kallats sinus-cosinus-formeln eller mellersta formeln.

Genom att utnyttja den polära dualitetssatsen på den ovanstående sinus-cosinus-formeln (samt att $\sin(\pi -x)=\sin x$ och $\cos(\pi -x)=-\cos x$) fås en "dual sinus-cosinus-formel":

$\sin(\pi -\beta )\cdot \cos(\pi -\alpha )=\cos(\pi -\beta )\cdot \sin(\pi -\alpha )\cdot \cos(\pi -c)+\sin(\pi -\gamma )\cdot \cos(\pi -a)\Leftrightarrow$

$-\sin \beta \cdot \cos \alpha =\cos \beta \cdot \sin \alpha \cdot \cos c-\sin \gamma \cdot \cos a\Leftrightarrow$

$\sin \gamma \cdot \cos a=\cos \beta \cdot \sin \alpha \cdot \cos c+\sin \beta \cdot \cos \alpha$

Eftersom allt som kan beräknas med hjälp av sinus-cosinus-formeln och dess dual även kan beräknas med sfäriska cosinussatsen eller duala cosinussatsen har sinus-cosinus-formlerna föga användning.