Sfäriska cosinussatsen
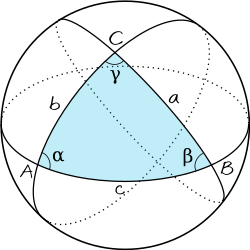
Den sfäriska cosinussatsen är en sats inom sfärisk trigonometri som säger att för en sfärisk triangel på en enhetssfär (en sfär med radien 1) gäller att (beteckningar enligt figur 1):
- och
Notera här att längden av storcirkelbågarna a, b, och c är lika med respektive vinkel i sfärens origo (O) i radianer, det vill säga , och , eftersom det är en enhetssfär. Om "sidlängderna" anges i radianer gäller satsen för sfäriska trianglar på alla sfärer.
Den sfäriska cosinussatsen är en sorts motsvarighet till plangeometrins cosinussats för trianglar och ju mindre den sfäriska triangeln är (det vill säga ju mindre vinklar i origo sidorna motsvarar), desto mer närmar sig sidorna räta linjer, och desto mer närmar sig den sfäriska cosinussatsen den plana cosinussatsen.
Om exempelvis är fås en sfärisk "motsvarighet" till Pythagoras sats[1] från den tredje ekvationen ovan:
Cosinus för "hypotenusan", det vill säga den motstående sidan till den räta vinkeln, är lika med produkten av cosinus för "kateterna", det vill säga det två övriga sidorna i den sfäriska triangeln.
Den sfäriska cosinussatsen har tillämpningar vid beräkningar på sfäriska ytor inom exempelvis astronomi, navigation och geodesi.
I den duala cosinussatsen har sidor och hörnvinklar "bytt plats" vilket ger en förvillande lik formel som lyder (beteckningar enligt figur 1):[2]
Härledning redigera
Härledning med skalärprodukt redigera
Givet den blå sfäriska triangeln på en enhetssfär med origo i i figur 2. Låt ett kartesiskt koordinatsystem ha origo i , vektorn definiera dess z-axel samt projektionen av på det mot z-axeln vinkelräta xy-planet definiera x-axelns riktning. Triangelsidorna , och motsvarar vinklarna , respektive och hörnvinkeln i är lika med (då sfärens tangentplan i är parallellt med xy-planet).
Eftersom och fås koordinaterna för triangelhörnen:
Skalärprodukten ges dels av:
och dels av:
vilket (med smärre omstuvning av högerledet) ger:
Härledning med elementär trigonometri redigera
Nedan ges ett enkelt geometriskt bevis baserat på elementär trigonometri för att i det fall inga "sidor" överstiger 90°. Bevis för övriga vinklar i triangeln är analoga.
Betrakta den röda sfäriska triangeln på en enhetssfär (med origo i ) i figur 3. I inledningen noterades att , och .
Eftersom det är en enhetssfär är .
Punkten är fotpunkt till på ytan , är fotpunkt till och på , är fotpunkt till och på och är fotpunkt till på .
Eftersom är en radie i sfären är vinkeln [3].
Då fås nu ur figur 3:
- (enligt ovan)
- (enligt ovan)
Samtidigt gäller att
där:
Så genom att sätta in formlerna (2), (3) och (4) i (1) och stuva om lite på ordningen fås alltså:
Om sammanfaller och och (då )
Det vill säga "den sfäriska varianten av Pythagoras sats".
Om (se figur 4) faller utanför vilket leder till:
- och
Uttrycken (2) och (3) ovan förblir oförändrade men i stället för (4) fås på grund av (6):
Så genom att sätta in (2), (3) och (7) i (5) (och återigen stuva om lite på ordningen) fås återigen:
Det kan också konstateras att en sfärisk triangel på en enhetssfär med alla sidor kortare än π/2 endast kan ha en hörnvinkel som är större än 90°.[4]
Om denna enda hörnvinkel som är större än 90° skulle vara vinkel α i figur 2, syns direkt att det inte påverkar härledningen. Skulle den vara β får härledningen göras utifrån B:s fotpunkt på ytan OAC i stället. γ visades ovan med hjälp av figur 4.
Det kan konstateras att satsen även gäller för "komplementtriangeln" (det icke blåfärgade området i figur 1). Denna har ju också sidlängderna a, b och c. Hörnvinklarna är dock de yttre vinklarna: 360°- α, 360° - β och 360° - γ. Men eftersom cos(360°-x)=cos(-x)=cos(x) gäller satsen.
Således är det visat att den sfäriska cosinussatsen gäller för alla sfäriska trianglar (på en enhetssfär) vars alla sidor är kortare än π/2.
Den duala cosinussatsen redigera
För den polära triangeln till (se figur 5) gäller:
Eftersom den sfäriska cosinussatsen även gäller för den polära triangeln får vi:
Samband mellan den sfäriska och den plana cosinussatsen redigera
I inledningen nämndes att då "sidorna" a, b och c representerar allt mindre vinklar i origo, så närmar sig den sfärsika cosinussatsen den plana. Så för mycket små vinklar a, b och c:
De båda maclaurinutvecklingarna:
kan skrivas som ("approximationerna för små vinklar"):
där är stora ordo.
Om vi applicerar detta på sinus och cosinus för a, b och c i den sfäriska satsen får vi:
Med [7] får vi:
De ordon som innehåller både a och b domineras antingen av eller av och kan därför inneslutas i antingen den ena eller andra av dessa och därför i deras summa.[8] Uttrycket kan sedan förenklas till
Tillämpningar redigera
Den sfäriska cosinussatsen kan användas för att beräkna en hörnvinkel om de tre sidorna i en sfärisk triangel är givna, eller beräkna den återstående sidan om två sidor och den mellanliggande hörnvinkeln är givna. Övriga hörnvinklar beräknas lämpligen med någon av de sfäriska cotangensformlerna eller med den sfäriska sinussatsen som är enklare.
Den duala cosinussatsen kan på motsvarande sätt användas om de tre hörnvinklarna är givna (till skillnad från en plan triangel är sidorna i en sfärisk triangel bestämda om alla tre hörnvinklarna är det) eller om två hörnvinklar och den mellanliggande sidan är given. Även här används lämpligen cotangensformlerna eller den sfäriska sinussatsen för att beräkna de båda övriga sidorna.
Övriga fall löses med hjälp av Napiers analogier.
Astronomi redigera
Inom astronomi kan den sfäriska cosinussatsen användas för att beräkna vinkelavståndet mellan två objekt på himmelssfären:
Betrakta den sfäriska triangeln med hörnet A i norra himmelspolen och hörnen B och C i respektive objekt (som i figur 2). Vinken α blir då lika med skillnaden i rektascension (RA) för objekten, medan b och c anger objektens polvinklar (b är polvinkeln för C, medan c är polvinkeln för B). Sidan a anger då vinkelavståndet θ mellan objekten. Alltså:
Eftersom polvinken är lika med , där betecknar deklinationen för objektet X, ger detta:
- där .
Om det ena objektet byts ut mot zenit, kan omvandlingar mellan ett objekts horisontella och ekvatoriella koordinater göras.
Geodesi redigera
På motsvarande sätt kan vinkelavstånd mellan orter på en sfärisk jord[9] beräknas (deklination motsvarar då latitud, , och rektascension longitud, ) och ur detta fås avståndet "fågelvägen" längs jordytan, genom att multiplicera med jordradien, :
redigera
För navigationsändamål gör denna kunskap om vinkelavståndet mellan farkostens nuvarande position och destinationen vidare att bäringen till destinationen kan beräknas med den sfäriska cosinussatsen. Så om A ligger i Nordpolen, C i positionen och B i destinationen fås bäringen ur γ (bäring betecknas även den liksom vinkelavståndet med θ, så här behålls γ för bäringen). Ekvationen för cos(c) stuvas därför om till:
där ( betecknar latitud):
- och
Insättning av uttrycken för b och c ger, efter förenkling:
Notera att vi får två olika bäringar inom 360°, dels γ och dels 360° - γ. Det första värdet gäller om destinationen ligger östligare än positionen, det andra om destinationen ligger västligare.
Notera även att nya bäringar kontinuerligt måste beräknas och kursen (i förhållande till kompassen/nordriktningen) läggas om allteftersom man färdas för att man skall fortsätta rakt fram längs storcirkeln och nå målet (om man inte följer en meridian eller ekvatorn), eftersom en storcirkel (ekvatorn undantagen) inte skär meridianerna i samma vinkel (en kurva som gör detta kallas loxodrom och leder i allmänhet[10] till att man i spiral närmar sig endera av polerna).
Övriga tillämpningar redigera
Solfångare och solpaneler redigera
Solstrålningens infallsvinkel för en plan solfångare eller solpanel kan beräknas med den sfäriska cosinussatsen[11] enligt:
- ,
eller, med och :
- ,
där är infallsvinkeln, och är zenitvinkeln för solen respektive solfångarens(-panelens) normalvektor, och är motsvarande höjdvinklar (altituder) och och är azimutvinklarna för solen respektive solfångarens normalvektor. (Azimuten anges vanligen i förhållande till sydriktningen på norra halvklotet vid solfångartillämpningar.[12])
Med beteckningar enligt figur 6 (z-axeln motsvarar lodlinjen och x- och y-axlarna spänner upp horisontalplanet): Vi har här en triangel på himmelssfären (vars medelpunkt, O, ligger på den grå solfångarens, eller -panelens, yta) som definieras av lodlinjen (riktningen till zenit, OA), riktningen till solen (OB) och solfångarpanelens normalvektor (OC). Infallsvinkeln är den vinkel (i) som solstrålningen bildar mot solfångarpanelens normalvektor. De båda övriga triangelsidorna utgörs av solens zenitvinkel (z) och panelnormalens zenitvinkel (zC). Vinkeln mellan dessa båda sidor i zenit (A) är skillnaden i azimut mellan solen (a) och panelnormalen (aC). Substitution av 90°-höjdvinkeln = zenitvinkeln via cos(90°-x) = sin(x) och sin(90°-x) = cos(x) ger den andra formeln ovan.
Historia redigera
Den sfäriska cosinussatsen förekommer i igenkännbar form hos Regiomontanus i bok fem av dennes De triangulis omnimodis från 1464, dock med användande av sinus versus i stället för cosinus.[13] I vilken mån Regiomontanus formulering är "densamma" som Al-Battanis (i Kitāb az-Zīj, cirka 900), och därför även huruvida Al-Battani rent av skall anses vara först med satsen, är något omdiskuterat.[14] Regiomontanus var väl förtrogen med Al-Battanis verk (och ägde själv två exemplar; varav det ena "återutgavs" med Regiomontanus kommentarer 1537), i vilket beräkning av solens azimut med hjälp av latituden, altituden och deklinationen på ett sätt som överensstämmer med satsen beskrivs.[15]
Referenser och noter redigera
- Spherical Trigonometry på MathWorld (ekvation 18-20).
- Torbjörn Tambour, 2015, Lite sfärisk geometri och trigonometri, sid. 3 - 4.
- ^ Cosinussatsen ger ju Pythagoras sats om en vinkel i triangeln är rät.
- ^ Tazim Ahsan, Änis Ben Hamida och Henrik Björk, 2009, Icke-euklidisk geometri i Projekt i matematisk kommunikation (PDF 7,2 MB), Lunds Tekniska Högskola, sid. 67.
- ^ Både och ligger ju i normalplan till .
- ^ Betrakta figur 1 och antag att hörnvinklarna α och β är 90°. Om storcirkeln genom A och B (och som innehåller sidan c) kallas "ekvator", så möts sidorna a och b i "nordpolen" och har båda längden π/2. Skulle α och β båda vara större än 90° skulle sidorna a och b mötas på andra sidan "nordpolen" vilket innebär att de båda också skulle vara längre än π/2. Detta gäller för den mot ABC stående triangeln med spetsen i C och hörnvinkeln γ som har sidlängderna π-a, π-b och c.
- ^ |O(x4)| < 0,1 ‰ av cos(x) om x < 0,22 rad (13°). Erik Ingelstam, Rolf Rönngern, Stig Sjöberg, 1971, TEFYMA, 1 uppl., 2 tr., Sjöbergs Förlag, sid. 66.
- ^ |O(x3)| < 0,1 ‰ av sin(x) om x < 0,025 rad (1,4°). TEFYMA, sid. 66.
- ^ Notera att vinklarna ("sidorna") a och b är mycket små så a2b2/4 är därför försumbart mycket mindre än a2/2 eller b2/2. Om a > b så dominerar a4 över a2b2 och är b > a så dominerar b4 över a2b2 - och vi har redan både O(a4) och O(b4) i ekvationen.
- ^ Notera att cos(γ)⋅O(x) = O(x). Om 1 > a > b så är a4 > a3b > a2b2 > ab3 > b4 > a2b4 > a4b4 (och motsvarande för 1 > b > a). Så antingen O(a4), O(b4) eller O(c4) dominerar över de övriga och felet kan således aldrig överstiga nio gånger den största av dessa tre. Och 9⋅O(x)=O(x).
- ^ Jorden är ju inte sfärisk, utan mer lik en rotationsellipsoid med avplattningen 1/300 (och referensgeoider mer komplicerade än så), så för noggrannare beräkningar krävs lite mer avancerad matematik. En beräkning med den sfäriska cosinussatsen av avståndet från Smygehuk (55,369° N, 13,351° E) till Treriksröset (69,060° N, 20,382°E), med jordradien 6361,5 km (för 62° N), resulterar i 1560,6 km. Enligt WGS-84 Geoid Distance Calculator Arkiverad 27 juli 2019 hämtat från the Wayback Machine. är avståndet 1566,6 km.
- ^ om inte vinkeln är 0°, då man följer en meridian, eller 90°, då man följer en parallell
- ^ Solar Incidence Angle på ScienceDirect.
- ^ Filippo Gualla, 2015, Sun position and PV panels: a model to determine the best orientation, Department of Physical Geography and Ecosystems Science, Lunds universitet, sid. 2.
- ^ versin α = 1 - sin(π/2 - α) [= 1 - cos α].
- ^ Tony Phillips, 2006 The True History of the Law of Cosines.
- ^ Ernst Zinner (övers. E. Brown), 2014, Regiomontanus: His Life and Work, sid. 57. ISBN 9781483295985.









