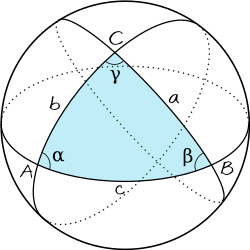
Delambres analogier

Delambres analogier, Delambres formler eller Delambres ekvationer, ibland kallade Gauss analogier , Gauss formler eller Gauss ekvationer, är en uppsättning formler inom sfärisk trigonometri. För en sfärisk triangel på en enhetssfär gäller (beteckningar enligt figur 1):

Figur 1.

${\begin{aligned}&\\{\frac {\sin {\frac {\alpha +\beta }{2}}}{\cos {\frac {\gamma }{2}}}}={\frac {\cos {\frac {a-b}{2}}}{\cos {\frac {c}{2}}}}&\qquad \qquad &{\frac {\sin {\frac {\alpha -\beta }{2}}}{\cos {\frac {\gamma }{2}}}}={\frac {\sin {\frac {a-b}{2}}}{\sin {\frac {c}{2}}}}\\[2ex]{\frac {\cos {\frac {\alpha +\beta }{2}}}{\sin {\frac {\gamma }{2}}}}={\frac {\cos {\frac {a+b}{2}}}{\cos {\frac {c}{2}}}}&\qquad &{\frac {\cos {\frac {\alpha -\beta }{2}}}{\sin {\frac {\gamma }{2}}}}={\frac {\sin {\frac {a+b}{2}}}{\sin {\frac {c}{2}}}}\end{aligned}}$

Motsvarande gäller även för övriga analoga kombinationer av hörnvinklar och sidor.

Utgående från ovanstående formler kan flera andra förhållanden inom den sfäriska trigonometrin visas, som exempelvis Napiers analogier.

De plantrigonometriska motsvarigheterna kallas Mollweides formler eller Mollweides ekvationer:

${\frac {\cos {\frac {\alpha -\beta }{2}}}{\sin {\frac {\gamma }{2}}}}={\frac {a+b}{c}}\qquad \qquad {\frac {\sin {\frac {\alpha -\beta }{2}}}{\cos {\frac {\gamma }{2}}}}={\frac {a-b}{c}}$

Härledningar

Delambres analogier med hjälp av de sfäriska formlerna för halva vinkeln

Från den plana trigonometrin har vi att

$\sin(x+y)=\sin x\cos y+\cos x\sin y$

vilket ger:

$\sin {\frac {\alpha +\beta }{2}}=\sin {\frac {\alpha }{2}}\cos {\frac {\beta }{2}}+\cos {\frac {\alpha }{2}}\sin {\frac {\beta }{2}}$

Vi expanderar nu högerledet med hjälp av de sfäriska formlerna för halva vinkeln:

$\sin {\frac {\alpha }{2}}={\sqrt {\frac {\sin(s{-}b)\sin(s{-}c)}{\sin b\sin c}}}\qquad$ och $\qquad \cos {\frac {\alpha }{2}}={\sqrt {\frac {\sin s\sin(s{-}a)}{\sin b\sin c}}}$

där $s={\frac {a+b+c}{2}}$

och motsvarande formler för ${\frac {\beta }{2}}$ vilket ger:

${\begin{aligned}\sin {\frac {\alpha +\beta }{2}}&={\sqrt {{\frac {\sin(s{-}b)\sin(s{-}c)}{\sin b\sin c}}\cdot {\frac {\sin s\sin(s{-}b)}{\sin a\sin c}}}}+{\sqrt {{\frac {\sin s\sin(s{-}a)}{\sin b\sin c}}\cdot {\frac {\sin(s{-}a)\sin(s{-}c)}{\sin a\sin c}}}}=\\&={\sqrt {\frac {\sin ^{2}(s-b)\sin(s-c)\sin s}{\sin a\sin b\sin ^{2}c}}}+{\sqrt {\frac {\sin ^{2}(s-a)\sin(s-c)\sin s}{\sin a\sin b\sin ^{2}c}}}=\\&={\frac {\sin(s-b)}{\sin c}}\cdot {\sqrt {\frac {\sin(s-c)\sin s}{\sin a\sin b}}}+{\frac {\sin(s-a)}{\sin c}}\cdot {\sqrt {\frac {\sin(s-c)\sin s}{\sin a\sin b}}}=\\&={\frac {\sin(s-b)+\sin(s-a)}{\sin c}}\cdot {\sqrt {\frac {\sin(s-c)\sin s}{\sin a\sin b}}}=\\&={\frac {\sin(s-b)+\sin(s-a)}{\sin c}}\cdot \cos {\frac {\gamma }{2}}\qquad (1)\end{aligned}}$

Där vi i sista steget utnyttjade denna sfäriska formel för halva vinkeln:

$\cos {\frac {\gamma }{2}}={\sqrt {\frac {\sin s\sin(s-c)}{\sin a\sin b}}}$

Från den plana trigonometrin har vi också att

$\sin x+\sin y=2\sin {\frac {x+y}{2}}\cos {\frac {x-y}{2}}$

vilket ger oss

${\begin{aligned}\sin(s-b)+\sin(s-a)&=2\sin {\frac {(s-b)+(s-a)}{2}}\cos {\frac {(s-b)-(s-a)}{2}}=\\&=2\sin {\frac {2s-b-a}{2}}\cos {\frac {a-b}{2}}=\\&=2\sin {\frac {c}{2}}\cos {\frac {a-b}{2}}\qquad (2)\end{aligned}}$

Där vi i sista steget utnyttjade

${\frac {2s-a-b}{2}}={\frac {2{\frac {a+b+c}{2}}-a-b}{2}}={\frac {a+b+c-a-b}{2}}={\frac {c}{2}}$

Från den plana trigonometrin har vi slutligen formeln för sinus för dubbla vinkeln:

$\sin c=2\sin {\frac {c}{2}}\cos {\frac {c}{2}}\qquad (3)$

Insättning av (2) och (3) i (1) ger oss:

$\sin {\frac {\alpha +\beta }{2}}={\frac {2\sin {\frac {c}{2}}\cos {\frac {a-b}{2}}}{2\sin {\frac {c}{2}}\cos {\frac {c}{2}}}}\cdot \cos {\frac {\gamma }{2}}={\frac {\cos {\frac {a-b}{2}}}{\cos {\frac {c}{2}}}}\cdot \cos {\frac {\gamma }{2}}\Leftrightarrow$

${\frac {\sin {\frac {\alpha +\beta }{2}}}{\cos {\frac {\gamma }{2}}}}={\frac {\cos {\frac {a-b}{2}}}{\cos {\frac {c}{2}}}}\qquad Q.E.D.$

De tre övriga analogierna visas analogt utgående från plantrigonometrins:

$\sin(x-y)=\sin x\cos y-\cos x\sin y$,

$\cos(x+y)=\cos x\cos y-\sin x\sin y$ respektive

$\cos(x-y)=\cos x\cos y+\sin x\sin y$

med användande av relevanta plantrigonometriska formler för de uttryck som uppstår samt, i två av fallen:

$\sin {\frac {\gamma }{2}}={\sqrt {\frac {\sin(s{-}b)\sin(s{-}a)}{\sin b\sin a}}}$

Delambres analogier med hjälp av Napiers analogier

Delambres analogier kan användas för att enkelt visa Napiers analogier men de kan också erhållas ur dessa. För det begränsade fallet att alla hörnvinklar och sidor är mindre än ${\frac {\pi }{2}}$ har vi.

Den sfäriska cosinussatsen

$\cos c=\cos a\cdot \cos b+\sin a\cdot \sin b\cdot \cos \gamma$

den plantrigonomtriska satsen för cosinus för dubbla vinkeln

$\cos \gamma =\cos ^{2}{\frac {\gamma }{2}}-\sin ^{2}{\frac {\gamma }{2}}$

trigonometriska ettan

$\cos ^{2}{\frac {\gamma }{2}}+\sin ^{2}{\frac {\gamma }{2}}=1$

samt därefter

$\cos(x-y)=\cos x\cos y+\sin x\sin y$

$\cos(x+y)=\cos x\cos y-\sin x\sin y$

ger oss:

${\begin{aligned}1+\cos c&=1+\cos a\cdot \cos b+\sin a\cdot \sin b\cdot \cos \gamma =\\&=\cos ^{2}{\frac {\gamma }{2}}+\sin ^{2}{\frac {\gamma }{2}}+\cos a\cdot \cos b\cdot (\cos ^{2}{\frac {\gamma }{2}}+\sin ^{2}{\frac {\gamma }{2}})+\sin a\cdot \sin b\cdot \left(\cos ^{2}{\frac {\gamma }{2}}-\sin ^{2}{\frac {\gamma }{2}}\right)=\\&=(1+\cos a\cos b+\sin a\sin b)\cos ^{2}{\frac {\gamma }{2}}+(1+\cos a\cos b-\sin a\sin b)\sin ^{2}{\frac {\gamma }{2}}=\\&=(1+\cos(a-b))\cos ^{2}{\frac {\gamma }{2}}+(1+\cos(a+b))\sin ^{2}{\frac {\gamma }{2}}\end{aligned}}$

Vi har också från den plana trigonometrin att

$1+\cos x=2\cos ^{2}{\frac {x}{2}}$

vilket nu appliceras trefalt på vårt uttryck:

$2\cos ^{2}{\frac {c}{2}}=2\cos ^{2}{\frac {a-b}{2}}\cos ^{2}{\frac {\gamma }{2}}+2\cos ^{2}{\frac {a+b}{2}}\sin ^{2}{\frac {\gamma }{2}}\Leftrightarrow$

$\cos ^{2}{\frac {c}{2}}=\cos ^{2}{\frac {a-b}{2}}\cos ^{2}{\frac {\gamma }{2}}+\cos ^{2}{\frac {a+b}{2}}\sin ^{2}{\frac {\gamma }{2}}\Leftrightarrow$

${\frac {\cos ^{2}{\frac {c}{2}}}{\cos ^{2}{\frac {a+b}{2}}\sin ^{2}{\frac {\gamma }{2}}}}={\frac {\cos ^{2}{\frac {a-b}{2}}\cos ^{2}{\frac {\gamma }{2}}}{\cos ^{2}{\frac {a+b}{2}}\sin ^{2}{\frac {\gamma }{2}}}}+1={\frac {\cos ^{2}{\frac {a-b}{2}}}{\cos ^{2}{\frac {a+b}{2}}}}\cdot \cot ^{2}{\frac {\gamma }{2}}+1=\tan ^{2}{\frac {\alpha +\beta }{2}}+1={\frac {1}{\cos ^{2}{\frac {\alpha +\beta }{2}}}}$

Där vi i näst sista steget utnyttjade Napiers analogi:

$\tan {\frac {\alpha +\beta }{2}}={\frac {\cos {\frac {a-b}{2}}}{\cos {\frac {a+b}{2}}}}\cdot \cot {\frac {\gamma }{2}}$

och i sista att

$\cos ^{2}x={\frac {1}{1+\tan ^{2}x}}$

Omflyttning ger oss:

${\frac {\cos ^{2}{\frac {\alpha +\beta }{2}}}{\sin ^{2}{\frac {\gamma }{2}}}}={\frac {\cos ^{2}{\frac {a+b}{2}}}{\cos ^{2}{\frac {c}{2}}}}$

Då vi begränsat oss till vinklar och sidor som alla är mindre än ${\frac {\pi }{2}}$ blir halva summan av två vinklar eller sidor också mindre än ${\frac {\pi }{2}}$ och samtliga cosinusvärden är därför positiva, varför vi utan problem kan dra roten ur vårt uttryck och få:

${\frac {\cos {\frac {\alpha +\beta }{2}}}{\sin {\frac {\gamma }{2}}}}={\frac {\cos {\frac {a+b}{2}}}{\cos {\frac {c}{2}}}}$

Härledningen av

${\frac {\cos {\frac {\alpha -\beta }{2}}}{\sin {\frac {\gamma }{2}}}}={\frac {\sin {\frac {a+b}{2}}}{\sin {\frac {c}{2}}}}$

görs analogt via

$2\sin ^{2}{\frac {c}{2}}=2\sin ^{2}{\frac {a-b}{2}}\cos ^{2}{\frac {\gamma }{2}}+2\sin ^{2}{\frac {a+b}{2}}\sin ^{2}{\frac {\gamma }{2}}$

De två återstående analogierna fås genom multiplikation av de två vi visat och två av Napiers analogier.

${\frac {\cos {\frac {\alpha +\beta }{2}}}{\sin {\frac {\gamma }{2}}}}={\frac {\cos {\frac {a+b}{2}}}{\cos {\frac {c}{2}}}}$

multiplicerad med

$\tan {\frac {\alpha +\beta }{2}}={\frac {cos{\frac {a-b}{2}}}{\cos {\frac {a+b}{2}}}}\cdot \cot {\frac {\gamma }{2}}$

ger

${\frac {\cos {\frac {\alpha +\beta }{2}}}{\sin {\frac {\gamma }{2}}}}\cdot \tan {\frac {\alpha +\beta }{2}}={\frac {\cos {\frac {a+b}{2}}}{\cos {\frac {c}{2}}}}\cdot {\frac {cos{\frac {a-b}{2}}}{\cos {\frac {a+b}{2}}}}\cdot \cot {\frac {\gamma }{2}}\Leftrightarrow$

${\frac {\cancel {\cos {\frac {\alpha +\beta }{2}}}}{\cancel {\sin {\frac {\gamma }{2}}}}}$$\cdot {\frac {\sin {\frac {\alpha +\beta }{2}}}{\cancel {\cos {\frac {\alpha +\beta }{2}}}}}={\frac {\cancel {\cos {\frac {a+b}{2}}}}{\cos {\frac {c}{2}}}}\cdot {\frac {cos{\frac {a-b}{2}}}{\cancel {\cos {\frac {a+b}{2}}}}}\cdot {\frac {\cos {\frac {\gamma }{2}}}{\cancel {\sin {\frac {\gamma }{2}}}}}\Leftrightarrow$

${\frac {\sin {\frac {\alpha +\beta }{2}}}{\cos {\frac {\gamma }{2}}}}={\frac {\cos {\frac {a-b}{2}}}{\cos {\frac {c}{2}}}}$

På samma sätt ger multiplikation av

${\frac {\cos {\frac {\alpha -\beta }{2}}}{\sin {\frac {\gamma }{2}}}}={\frac {\sin {\frac {a+b}{2}}}{\sin {\frac {c}{2}}}}$

med

$\tan {\frac {\alpha -\beta }{2}}={\frac {sin{\frac {a-b}{2}}}{\sin {\frac {a+b}{2}}}}\cdot \cot {\frac {\gamma }{2}}$

till resultat

${\frac {\sin {\frac {\alpha -\beta }{2}}}{\cos {\frac {\gamma }{2}}}}={\frac {\sin {\frac {a-b}{2}}}{\sin {\frac {c}{2}}}}$

Mollweides formler

Då storcirkelbågarna (triangelsidorna) i en sfärisk triangel görs allt mindre närmar dessa sig räta linjer och den sfäriska triangeln närmar sig en plan triangel. Då ${\frac {\sin x}{x}}\rightarrow 1$ när $x\rightarrow 0$ följer Mollweides formler ur de två av Delambres analogier som står till höger i artikelns inledning.

Men Mollweides formler kan även visas helt plantrigonometriskt med hjälp av den planära sinussatsen:

${\frac {a}{\sin \alpha }}={\frac {b}{\sin \beta }}={\frac {c}{\sin \gamma }}$

Vi har:

${\frac {a-b}{c}}={\frac {a}{c}}-{\frac {b}{c}}={\frac {\sin \alpha }{\sin \gamma }}-{\frac {\sin \beta }{\sin \gamma }}={\frac {\sin \alpha -\sin \beta }{\sin \gamma }}$

De kända formlerna

$\sin \alpha -\sin \beta =2\cos {\frac {\alpha +\beta }{2}}\sin {\frac {\alpha -\beta }{2}}$ och

$\sin 2\gamma =2\sin \gamma \cos \gamma \Leftrightarrow \sin \gamma =2\sin {\frac {\gamma }{2}}\cos {\frac {\gamma }{2}}$

ger:

${\frac {a-b}{c}}={\frac {2\cos {\frac {\alpha +\beta }{2}}\sin {\frac {\alpha -\beta }{2}}}{2\sin {\frac {\gamma }{2}}\cos {\frac {\gamma }{2}}}}$

och $\alpha +\beta +\gamma =\pi$ och därefter $\cos({\frac {\pi }{2}}-x)=\sin x$ ger oss:

${\frac {a-b}{c}}={\frac {2\cos {\frac {\pi -\gamma }{2}}\sin {\frac {\alpha -\beta }{2}}}{2\sin {\frac {\gamma }{2}}\cos {\frac {\gamma }{2}}}}={\frac {2\sin {\frac {\gamma }{2}}\sin {\frac {\alpha -\beta }{2}}}{2\sin {\frac {\gamma }{2}}\cos {\frac {\gamma }{2}}}}={\frac {\sin {\frac {\alpha -\beta }{2}}}{\cos {\frac {\gamma }{2}}}}$

Den andra formeln visas analogt.

Historia

Jean-Baptiste Joseph Delambre publicerade sin upptäckt med ett geometriskt bevis i den franska astronomiska almanackan Connaissance des Temps för 1809, utgiven i april 1807. Den 28 mars 1809, och oberoende av Delambre, publicerade Carl Friedrich Gauss analogierna utan bevis i Theoria motus corporum coelestium in sectionibus conicis solem ambientium. I tyskspråkiga länder kallas de därför ofta för "Gauss analogier" (Gaußsche Gleichungen), trots att Delambre bevisligen har företräde.

Carl Brandan Mollweide publicerade sina formler 1808 i Zusätze zur ebenen und sphärischen Trigonometrie..

Referenser och noter

• Isaac Todhunter, 1886, Spherical Trigonometry: For the Use of Colleges and Schools, Macmillan & Co, sid. 26-27 (artikel 54-55). Faksimil PDF (3 MB), TeX PDF (789 kB). 1883 års upplaga online på Google Books.
• Robert E.Moritz, 1913, A Text Book On Spherical Trigonometry, John Wiley And Sons, sid. 43-44.