Matematisk induktion

Matematisk induktion är en bevismetod som tillämpas på påståenden som omfattar mängden av naturliga tal som är större än eller lika med ett startvärde (till exempel 0 eller 1). Då mängden naturliga tal är obegränsad kan bevis inte utföras för varje enskilt fall. I det generella induktionsbeviset delas beviset för påståendet upp i tre steg:

• Induktionsbasen: först visas att påståendet är sant för ett startvärde, till exempel för heltalet n = 1
• Induktionsantagandet: utsagan antas vara sann för något heltal n
• Induktionssteget: visa att om induktionsantagandet är sant, så är påståendet också sant för n + 1

Illustration av induktionsbevis

En informell beskrivning av matematisk induktion kan illustreras med fallande dominobrickor

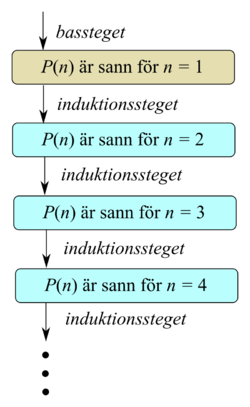
När dessa steg är utförda är det bevisat att påståendet gäller för alla n från och med det antagna startvärdet. Tekniken kan även tillämpas på de matematiska objekt som är vidareutvecklingar av de positiva heltalen, ordinaltalen.

Denna bevismetod är av grundläggande betydelse för aritmetik och mängdlära och därmed för alla områden av matematiken.

Tekniken kan illustreras med dominobrickor: varje dominobricka är ställd på högkant och representerar ett tal i den ordnade följden av positiva heltal. Om en bricka välter, välter den också den nästföljande brickan. Induktionsprincipen innebär att samtliga dominobrickor kommer att bli välta om den första brickan har blivit vält.

Definitioner

Låt P(n) vara ett påstående som har att göra med ett positivt heltal n och antag att detta påstående är sant. Om

• $P(1)$ är sant
• $\forall p\in \mathbb {N} :P(p)\Rightarrow P(p+1)$

så är påståendet P(n) sant för varje positivt heltal n.

Informell definition

Låt A vara en mängd som innehåller talet 1 och som även innehåller talet n + 1 om det innehåller det positiva heltalet n. Mängden A är då lika med mängden av alla positiva heltal.

Vanligtvis formuleras principen för matematisk induktion som ett axiom för de naturliga talen, som till exempel inom Peanos axiomsystem. Det är emellertid möjligt att inom vissa formella system härleda principen från andra antaganden, till exempel att mängden av naturliga tal är en välordnad mängd. Exempel:

Bevis med hjälp av välordningsaxiomet

Det övergripande beviset kan utföras med en matematisk metod som kallas motsägelsebevis (latin: Reductio ad absurdum). Först antas att motsatsen till det som skall bevisas är sann och sedan visas att detta leder till en motsägelse; ett påstående som inte kan vara sant:

Antag att A inte är lika med mängden av alla positiva heltal. Då finns positiva heltal som inte tillhör mängden A. Antag att dessa är elementen i mängden B; en icke-tom mängd bestående av positiva heltal. Enligt välordningsaxiomet för de positiva heltalen innehåller B ett minsta element, m.

Eftersom mängden A innehåller talet 1, kan elementet m inte vara talet 1; det är därför större än talet 1. Då är elementet m - 1 ett positivt heltal som är mindre än talet m. Talet m - 1 kan inte tillhöra mängden B, eftersom m - 1 då vore det minsta elementet i B. Därför måste talet m - 1 tillhöra mängden A. Men om elementet m - 1 ligger i mängden A, ligger det efterföljande talet (m - 1) + 1 också i mängden A, det vill säga att talet m ligger i mängden A.

Det finns således ett element m, som både tillhör och inte tillhör mängden A, vilket är en motsägelse.

Det var därför fel att anta att mängden A inte var lika med mängden av positiva heltal. Principen om matematisk induktion är därmed bevisad.

Exempel

Induktionsbevis används ofta för att bevisa att något är sant för alla naturliga tal.

Aritmetisk talföljd

Sats

Om $n$ är ett positivt heltal så är summan

$1+2+3+\cdots +n={\frac {n(n+1)}{2}}$

Bevis

1. Visa först att satsen gäller för $n=1$:

Om $n=1$ så är vänsterledet

$1$

och högerledet är

${\frac {n(n+1)}{2}}={\frac {1\cdot (1+1)}{2}}={\frac {2}{2}}=1$

Alltså stämmer satsen då $n=1$.

2. Antag att satsen stämmer för det positiva heltalet $n$

3. Det gäller då att visa att satsen stämmer för nästa heltal, $n+1$, det vill säga, att visa att

$1+2+3+\cdots +n+(n+1)={\frac {(n+1)(n+2)}{2}}$

Genom att gruppera om termerna i summan går det att tillämpa induktionsantagandet:

$1+2+3+\cdots +n+(n+1)=(1+2+3+\cdots +n)+(n+1)=$

$={\frac {n(n+1)}{2}}+(n+1)=(n+1)(1+{\frac {n}{2}})={\frac {(n+1)(n+2)}{2}}$

Satsen stämmer för det positiva heltalet 1. Om satsen stämmer för det positiva heltalet $n$, så stämmer satsen för nästa positiva heltal, $n+1$. Enligt principen för matematisk induktion stämmer därmed satsen för alla positiva heltal.

V.S.B.

Tal på formen $3^{2n+1}+5^{2n}$ är delbara med 4, men inte med 8

Det går också att göra tvärtom och visa att om ett påstående är falskt för n = p, är det även falskt för n = p + 1:

Påstående:

För varje naturligt tal n är talet $3^{2n+1}+5^{2n}$ delbart med 4, men inte med 8.

Bevis:

Förenkling ger $k=3^{2n+1}+5^{2n}=3\cdot 3^{2n}+5^{2n}=3\cdot 9^{n}+25^{n}$

För n = 0 gäller alltså att $k_{0}=3+1=4$ och för n = 1 att $k_{1}=3\cdot 9+25=52$. Både 4 och 52 är delbara med 4, men inte med 8. Det är nu visat för två basfall.

Antag att påståendet (delbarhet med 4) är sant för n = p + 1, alltså för $k_{p+1}=27\cdot 9^{p}+25\cdot 25^{p}$; då gäller för n = p + 2:

$k_{p+2}=27\cdot 9^{p+1}+25\cdot 25^{p+1}$

$k_{p+2}=27\cdot 9^{p+1}+25\cdot 25^{p+1}+216\cdot 9^{p}-216\cdot 9^{p}+600\cdot 25^{p}-600\cdot 25^{p}$

$k_{p+2}=(27\cdot 9^{p}+25\cdot 25^{p})+216\cdot 9^{p}+600\cdot 25^{p}$

Parentesen motsvarar antagandet, alltså delbarhet med 4. 216 och 600 är båda delbara med 4 och således är även hela uttrycket delbart med 4. Induktionsprincipen ger att $3^{2n+1}+5^{2n}$ är delbart med 4 för alla naturliga tal n.

Om vi antar att $k_{p+1}$ är delbart med 8 visar det alltså sig att även $k_{p+2}$ är delbart med 8, eftersom 216 och 600 är delbara med 8. Problemet här är att vi inte kan påbörja induktionen eftersom vi inte har något basfall. Om vi däremot hade antagit att det var falskt för $k_{p+1}$, hade vi funnit med samma metod som ovan att det även är falskt för $k_{p+2}$. Då det är falskt (delbarhet med 8) för basfallen n = 0 och n = 1, innebär induktionsprincipen att $3^{2n+1}+5^{2n}$ inte är delbart med 8 för alla naturliga tal n och det ursprungliga påståendet har bevisats.

Hur stort är talet n-fakultet?

För att få en uppfattning om storleken hos talen $n$-fakultet ($n!$) skall vi visa att:

$n!\leq n^{n},\qquad n=1,2,3,\dots \,.$

Induktionsbasen

För det första gäller olikheten då $n=1$, eftersom $1!=1$.

Induktionsantagandet

Vi antar att olikheten gäller för talet $n=N$.

Induktionssteget

Vi skall nu visa att olikheten även gäller för nästa heltal, $N+1$.

$(N+1)!=N!\,(N+1)\leq N^{N}\,(N+1)\leq (N+1)^{N}\,(N+1)=(N+1)^{N+1}.$

Enligt principen för matematisk induktion gäller därför olikheten för alla positiva heltal: $1,2,3,\dots$

Se även

• Peanos axiom
• Zorns lemma
• Induktion (filosofi)
• Lista över matematiska symboler
• Mathematical induction