Runges fenomen
Runges fenomen uppträder då man inom matematiken anpassar polynom av hög grad till ett antal mätpunkter i planet. Fenomenet innebär att kurvan kommer att svänga kraftigt mellan interpolationspunkterna, ju högre grad på polynomet desto kraftigare svängningar. Runges fenomen är uppkallat efter den tyske matematikern Carl Runge
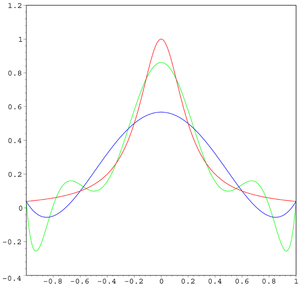
Effekten kan minimeras genom att välja nollställen till ortogonala polynom (särskilt Tjebysjovpolynom) som interpolationspunkter i stället för jämnt spridda punkter. Interpolering med rationella funktioner undviker problemet helt. Ytterligare ett alternativ är att använda splines.