Skalärprodukt
Skalärprodukt, också kallad inre produkt, är inom vektoralgebran en operation på två vektorer a och b vars resultat är en skalär och som i ett euklidiskt rum kan definieras som[1]
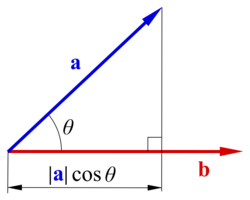
där θ är vinkeln mellan vektorerna. Skalärprodukten kan tolkas som längden av a:s projektion på b multiplicerad med b:s längd.
Om vektorernas komponenter är kända i en ortonormerad bas kan skalärprodukten även ges en algebraisk definition
Definition redigera
En skalärprodukt kan definieras algebraiskt eller geometriskt. Den geometriska definitionen är grundad på begrepp som vinklar och avstånd (vektorers magnitud). Ekvivalensen mellan dessa två definitioner kräver ett kartesiskt koordinatsystem i det euklidiska rummet.
I moderna framställningar av euklidisk geometri, är punkterna i rummet kartesiska koordinater och det eukldiska rummet självt är vanligen identifierat med den reella koordinatrymden Rn. I en sådan framställning, är begreppen längd och vinklar definierade med hjälp av skalärprodukten. En vektors längd är definierad som kvadratroten av skalärprodukten av en vektor med sig själv och cosinus av den icke orienterade vinkeln mellan två vektorer av längd 1, är definierad som deras skalärprodukt. Ekvivalensen av de två definitionerna av skalärprodukt är en del av ekvivalensen mellan den klassiska och de moderna framställningarna av euklidisk geometri.
Algebraisk definition redigera
Skalärprodukten av två vektorer a = [a1, a2, …, an] och b = [b1, b2, …, bn] är definierad som:[2]
där Σ betecknar summation och n vektorrummets dimension. Till exempel, i ett tredimensionellt rum, är skalärprodukten av vektorerna [1, 3, −5] och [4, −2, −1]
Om vektorerna identifieras med radmatriser, kan skalärprodukten även skrivas som matrisprodukten
där betecknar transponatet av .
Uttryckt på detta sätt, är en 1 × 3 matris (radvektor) multiplicerad med en 3 × 1 matris (kolumnvektor) en 1 × 1 matris
Geometrisk definition redigera
I ett euklidiskt rum, är en euklidisk vektor ett geometriskt objekt som har både en storlek och en riktning. En vektor kan avbildas som en pil. Dess storlek är dess längd och dess riktning är riktningen i vilket pilen pekar. Magnituden av en vektor a betecknas som . Skalärprodukten av två euklidiska vektorer a och b är definierad som[3][4]
där θ är vinkeln mellan a och b.
Om vektorerna a och b är ortogonala (deras mellanliggande vinkel är π / 2 eller 90°) och då , vilket implicerar
Vid den andra ytterligheten, om de är motriktade, är vinkeln mellan dem 0
Detta implicerar att skalärprodukten av en vektor a med sig själv är
som ger
vilket är formeln för en vektors euklidiska längd.
Egenskaper redigera
Om a, b och c är reella vektorer är skalärprodukten kommutativ
Skalärprodukten är skalbar i båda variablerna, det vill säga, för varje skalär α:
Den är också distributiv:
vilket kan sammanfattas som att den skalära produkten är en bilinjär form. Den är dessutom positivt definit, vilket innebär att aldrig är negativ och är noll om och endast om , nollvektorn.
De algebraiska och geometriska definitionerna är ekvivalenta redigera
Om e1, ..., en är standardbasvektorer i Rn, kan vi skriva
Vektorerna ei är en ortonormal bas, vilket innebär att de är av enhetslängd och är inbördes vinkelräta mot varandra. Således, då dessa vektorer är av enhetslängd
och är rätvinkliga mot varandra och om i ≠ j, är
Således gäller i allmänhet
där δ ij är Kroneckerdeltat.
Dessutom, i enlighet med den geometriska definitionen, för varje vektor ei och en vektor a gäller
där ai är komponenten av vektorn a i riktningen ei.
Applicera distributiviten på den geometriska versionen av skalärprodukten:
vilket är den algebraiska definitionen av skalärprodukten. Alltså är den geometriska skalärprodukten ekvivalent med den algebraiska skalärprodukten.
Exempel redigera
Tillämpning på cosinussatsen redigera
Givet två vektorer a och b åtskilda av en vinkel θ, som bildar en triangel med en tredje sida c = a − b. Skalärprodukten av c med sig själv är
vilket är cosinussatsen.
Inom fysiken redigera
Inom fysiken är vektorlängderna en skalär i fysikalisk mening, det vill säga, en fysikalisk storhet som är oberoende av koordinatsystemet, uttryckt som en produkt av ett numeriskt värde och en fysikalisk enhet, inte bara som ett tal. Skalärprodukten är också en skalär i denna mening, den är oberoende av koordinatsystemet. Exempel är:[5][6]
- Mekaniskt arbete är skalärprodukten av kraft och förskjutningvektor
- Effekt är skalärprodukten av kraft och hastighet
Komplexa vektorer redigera
För vektorer med komplexa tal som komponenter, leder den gängse definitionen av skalärprodukten till avvikande egenskaper. Till exempel, skalärprodukten av en vektor med sig själv är ett godtyckligt komplext tal och kan vara noll utan att vektorn är nollvektorn, vilket i sin tur har konsekvenser för begrepp som längder och vinklar. Egenskaper som den positiva-definita normen kan offras till priset av att ge upp de symmetriska och bilinjära egenskaperna hos skalärprodukten genom den alternativa definitionen[7]
där bi är komplexkonjugatet av bi. Då är skalärprodukten av en vektor med sig själv ett icke-negativt reellt tal och är nollskilt med undantag för nollvektorn. Emellertid är denna skalärprodukt sesquilinjär snarare än bilinjär: den är linjär i sin konjugerade form och icke-linjär i a och inte symmetrisk eftersom
Vinkeln mellan två komplexa vektorer ges då av
Denna typ av skalärprodukt är inte desto mindre användbar och leder bland annat till generella definitioner av inre produktrum.
Se även redigera
Referenser redigera
- ^ Weisstein, Eric W. "Dot Product." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/DotProduct.html
- ^ S. Lipschutz; M. Lipson (2009). Linear Algebra (Schaum’s Outlines) (4th). McGraw Hill. ISBN 978-0-07-154352-1.
- ^ M.R. Spiegel; S. Lipschutz; D. Spellman (2009). Vector Analysis (Schaum’s Outlines) (2nd). McGraw Hill. ISBN 978-0-07-161545-7.
- ^ A I Borisenko; I E Taparov (1968). Vector and tensor analysis with applications. Dover. Sid. 14.
- ^ K.F. Riley; M.P. Hobson; S.J. Bence (2010). Mathematical methods for physics and engineering (3rd). Cambridge University Press. ISBN 978-0-521-86153-3. https://archive.org/details/mathematicalmeth00rile.
- ^ M. Mansfield; C. O’Sullivan (2011). Understanding Physics (4th). John Wiley & Sons. ISBN 978-0-47-0746370.
- ^ Berberian, Sterling K. (2014) [1992], Linear Algebra, Dover, s. 287, ISBN 978-0-486-78055-9
Externa länkar redigera
- Wikimedia Commons har media som rör Skalärprodukt.

