Lamberts W-funktion
| Den här artikeln behöver källhänvisningar för att kunna verifieras. (2020-04) Åtgärda genom att lägga till pålitliga källor (gärna som fotnoter). Uppgifter utan källhänvisning kan ifrågasättas och tas bort utan att det behöver diskuteras på diskussionssidan. |
Lamberts W-funktion är en matematisk funktion som används för att lösa ekvationer innehållande logaritmer eller exponentialfunktioner som inte kan elimineras algebraiskt. Den betecknas W och definieras som inversen till funktionen
där w är ett komplext tal och ew betecknar exponentialfunktionen. Lamberts W-funktion är uppkallad efter den schweizisk-preussiske matematikern och fysikern Johann Heinrich Lambert.
Flervärdhet redigera
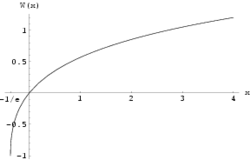
Funktionen
är inte injektiv på (−∞, 0) och W är därför en flervärd funktion på [−1/e, 0). För reella argument x ≥ −1/e kan man med kravet w ≥ −1 definiera en entydig funktion W0. Denna funktion uppfyller W0(0) = 0 och W0(−1/e) = −1.
Metod för ekvationslösning redigera
Lamberts W-funktion uppfyller
och kan därför tillämpas genom att man skriver om ekvationer på formen där c är konstant, varefter lösningen ges av . Exempelvis kan ekvationen 2t = 5t lösas genom omskrivningen
Specifika ekvationer och värden redigera
De ekvivalenta ekvationerna och har lösningen
Ekvationen löses av
och det oändliga tornet av potenser
antar vid konvergens värdet
Några specifika värden är
- (omegakonstanten)
- .
Taylorserie redigera
Maclaurinserien till Lamberts W-funktion kan beräknas utifrån den implicita ekvationen
genom Lagranges inverteringssats. Resultatet är
som enligt kvottestet har konvergensradien 1/e.
Mer allmänt, för är
Derivata och primitiv funktion redigera
Derivatan ges av
- .
Många uttryck innehållande Lamberts W-funktion kan integreras genom variabelsubstitutionen w = W(x), det vill säga x = w ew. Speciellt gäller
Differentialekvation redigera
Lamberts W-funktion uppfyller differentialekvationen
Övriga formler redigera
Tillväxt redigera
En approximation av för stora är
Externa länkar redigera
- Wikimedia Commons har media som rör Lamberts W-funktion.
